 |
| Combined Footing Design Calculation in Excel Spreadsheet |
Hey, I'm Engr. BalaRam, Today I share How to design combined footing by Ultimate Strength Design(USD) method. You can download this design calculation Spreadsheet in free.
How to Design Combined Footing?
This Excel Spreadsheet helps you with the design of combined footing. Following parts are considered in it to perform the Size of the Footing:
- Size of combined footing.
- Combined footing design in the longitudinal direction.
- Combined footing design in a cross direction.
Step -01: Input your data For Example:
Step -02: Footing Size
Since the space between the bottom of the footing and the surface will be occupied partly by concrete and partly by soil (fill), the average unit weight of 125 lb/ft3 will be assumed.
So, Pressure of Soil, A1 = 125.00 pcf.
Let, Top of the Footing below GL, B1 = 8.00 ft.
The Soil Pressure at 8.00 ft depth, C1= A1xB1 = 1,000.00 psf.
Step -03: Calculating S.F & B.M at Different Points
Factored Load on Colm.A, PuA= 254.00 kips (Load taken from Staadpro)
Factored Load on Colm.B, PuB= 267.00 kips (Load taken from Staadpro)
Factored Load from Colms, Pu = 521.00 kips.
Upward pressure caused by the factored load of the column, Qu = Pu / (LxB) = 3.02 ksf.
The Net Upward pressure per linear foot in the longitudinal direction is,
Wu = Qu*B kips/ft. = 28.16 kips/ft.
 |
| Calculating S.F & B.M at Different Points |
Step -04: Checking "d" from Punching Shear
Let, the depth of the footing, d = 15.50 in 1.29 ft.
Punching shear should be checked on a perimeter section st a distance d/2 around the column.
Of the two columns, the left side column (Col.A) is more critical at a distance d/2 from the column face in regard to the punching shear.
Step -05: Checking "d" from Beam Shear
The selected value d= 15.50 inches will now be checked for one-way or beam shear at a distance "d" to the left side of Column B. The factored shear force acting on that section is:-
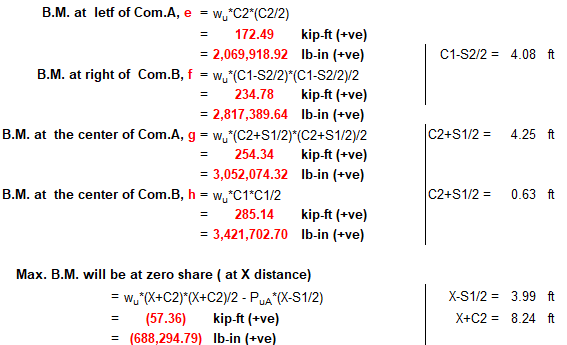
Step -06: Checking "d" from Maximum Moment
Step -07: Steel Requirements in the Long Direction (L) (Top Bar)
 |
| Steel Requirements in the Long Direction |
The distance from the point of Max. Moment to the nearer left end of the bar is:-
= X+C2-3/12 (deducting 3" clear cover) = 7.99 ft.
Which is much larger than the required minimum development length. So, the selected reinforcement is therefore adequate for both bending and bond.
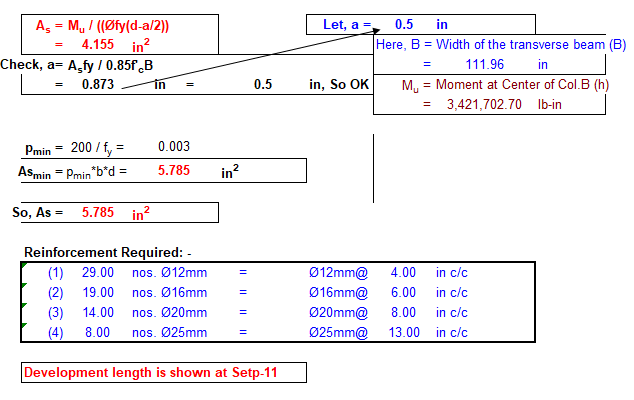
Step -11: Steel requirements under Column "A" (Longitudinal)
 |
| Reinforcement Required |
Step -12: Steel requirements under Column "B" (Longitudinal)
Step -13: Design of Transverse Beam Under Column."A"
From Step-11, the width of the transverse beam under Col.A, b= 2.15 ft.
Since the transverse reinforcement is placed on the top of the longitudinal bars, the actual depth will be, d= Actual "d" - 1 in = 14.50 in
Factored Load on Colm.A, PuA= 254.00 kips.
Width of the Footing, B = 9.33 ft.
The net upward load per linear foot of the transverse beam, WuA = PuA / B
= 27.22 kip/ft = 27,224.01 lb/ft.
The moment at the edge of Col.A, Mu = WuA*X1*(X1/2)
X1= B/2 - Z1/2
= 236,130.50 lb-ft. = 4.17 ft.
Step -14: Design of Transverse Beam Under Column."B"
From Step-11, the width of the transverse beam under Col.B, b= 2.13 ft.
Since the transverse reinforcement is placed on the top of the longitudinal bars, the actual depth will be, d= Actual "d" - 1 in = 14.50 inches.
Factored Load on Colm.B, PuB= 267.00 kips
Width of the Footing, B = 9.33 ft.
The net upward load per linear foot of the transverse beam, WuB = PuB / B
= 28.62 kip/ft = 28,617.36 lb/ft.
The moment at the edge of Col.A, Mu = WuB*X2*(X2/2)
X2= B/2 - Z2/2
= 233,540.58 lb-ft. = 4.04 ft.
Step -15: Development Length for Column
Where D = Dia of Footing Reinforcement.
Where, SO = Perimeter of Reinf.
= 2*P*r
= P*d
P = 3.14
Download file: Combined footing Design Excel sheet ACI 318. I'm also a shared Isolated Column Footing Design Excel Spreadsheet in my previous post.
We hope that this excel sheet to design Combined Footing will be useful to professionals and students of civil engineering, always keep in mind good criteria when using any type of design software. Do not forget to share this design on your social networks, with your support. We reach more people interested in the different areas of civil engineering. We wait for your comments and opinions, Greetings to all. Thank you.






















5 Comments
hi
ReplyDeleteHow can I help you??
DeleteSuch an amazing blog balram, keep sharing, I have also written a blog post on Fly Ash Bricks vs Red Bricks
ReplyDeleteThank you..
DeleteIf you want to contact the tiles exporter, then you can buy tiles from our website and export them, which will give you many benefits.
ReplyDelete