Slab design calculation one way and two way method in excel sheet with example

Civil or structural engineer know that how to calculated slab design. Here you can get a free excel sheet where a engineer easily design one way or two way slab by one click. We also explain a slab design example in this excel sheet. 

Download this Excel Sheet: Slab design calculation excel sheet

(only download and open your device / no needed password)

Slab design calculation one way and two way method:

An Example of two way design calculation:

Input data:

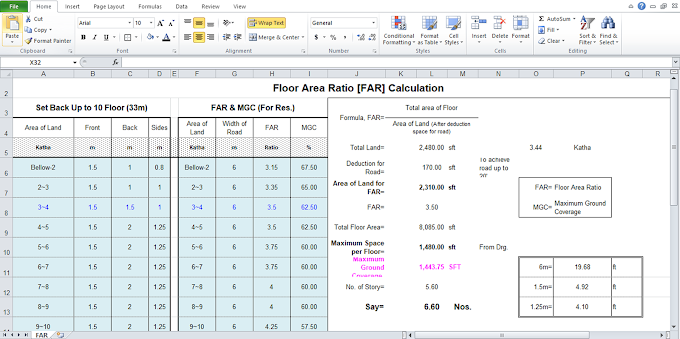
Slab Dimensions:

Short span = 10 ft.
Long Span = 15 ft.
Span ratio = 10/15 = 0.67
Slab thickness (reqd) = 2 x (10+15) x 12/180 = 3.33 in
Slab thickness (prvd) = 5 in.


Edge Conditions:

Short span edge condition = Both edges continuous
Long span edge condition = Both edges discontinuous

Applied Loads: 

Slab self wt = 62.50 psf.
Service dead load = 40 psf.
Service live load = 75 psf.
Material Strengths:
Concrete Strength = 2.5 ksi.
Steel yield strength = 60 ksi.

Design Moments

Loads:

Total ultimate DL = 1.4x(62.5+40) = 143.5 psf.
Total ultimate LL = 1.7x(75) = 127.5 psf.
Total ultimate load = 143.5+ 127.5 = 271 psf.

Short Span Moments:

Positive Moment DL Muall(dl)+ = 0.036 x 143.5 x 10^2 = 0.517 k-ft.
Positive Moment LL Muall+ = 0.054 x 127.5 x 10^2 = 0.689 k-ft.
Total positive short span moment mua+ = 1.205 k-ft.
Negative Moment on Discontinuous Edge = 1/3 x 0.416 = 0.139 k-ft.
Negative Moment on Discontinuous Edge = 1/3 x 0.416 = 0.139 k-ft.

Reinforcement Calculations

Shear Check:

Total load on the panel = 10 x 15 x 288.5 = 43.2 kips

Shear Capacity of the section fVc = 0.85 x 2 x ( 2500 )^½ x 12 x 5 / 1000 

    = 5.1 k/ft

Shear along short side      Vua  =  ( 0.04 x 43.2 ) / (2 x 10 ) 

= 0.08 k/ft    <5.1 k/ft…. (O.K.)

Shear along short side      Vub =( 0.04 x 43.2 ) / (2 x 10 )

 = 0.08 k/ft <5.1 k/ft…. (O.K.)

Short Span Moments:

Positive Moment DL Mua(dl)+ = 0.036 x 161 x 10^2  = 0.580 k-ft

Positive Moment LL Muall+ = 0.054 x 127.5 x 10^2 = 0.689 k-ft

Total Postive Short Span Moment Mua+ =  1.268 k-ft

Negative Moment on Continuous Edge = 0.087 x 288.5 x 10^2  = 2.510  k-ft

0.087 x 1.268

0.087 x 288.5 x 10^2

Negative Moment on Continuous Edge = 0.087 x 288.5 x 10^2 = 2.510 k-ft

0.087 x 1.268

0.087 x 288.5 x 10^2

Long Span Moments:

Positive Moment DL Mubdl+ = 0.004 x 161 x 15^2  = 0.145 k-ft

Positive Moment LL Mubll+ = 0.01 x 127.5 x 15^2  = 0.287 k-ft

Total Postive Long Span Moment Mub+  = 0.432  k-ft

Negative Moment on Discontinuous Edge = 1/3 x 0.432 = 0.144 k-ft

1/3 x 0.432

1/3 x 288.5 x 15^2

Negative Moment on Discontinuous Edge = 1/3 x 0.432 = 0.144 k-ft

1/3 x 0.432

1/3 x 288.5 x 15^2

If you insert One way slab data. then this calculation result show for one way slab. 

You can also downloads  

One way slab design example pdf

Two way slab design example pdf

Example: Let's say we have a one-way slab with dimensions 5m x 4m and a total load of 20 kN/m². Using Excel, we input these values into our table, and it automatically calculates the bending moment and required reinforcement based on standard formulas.

For a two-way slab, let's consider a 6m x 6m slab with the same load. We'll distribute the load accordingly, calculate bending moments for both directions, and determine the required reinforcement.

By creating Excel sheets for both one-way and two-way slab designs, engineers can efficiently calculate and optimize slab designs for construction projects.

More Excel Sheet free download: Calculate The Quantity of slab Reinforcement

In conclusion, designing slabs, whether one-way or two-way, involves understanding the loads they will bear and calculating the bending moments to determine the required reinforcement. In Excel, engineers can create tables to input dimensions and loads, which automatically calculate bending moments and reinforcement based on standard formulas. This helps streamline the design process and ensures that slabs meet safety and structural requirements for construction projects.